온라인 저지, 알고리즘 대회 등에서 문제를 출제할 때 출제자의 의도에 맞는 효율적인 구조로 유도하기 위해 적절한 시간 제한을 두기 때문에, 알고리즘 설계 시 시간 복잡도를 고려하여 작성해야 한다.
알고리즘의 분석 기준
알고리즘의 성능을 분석하는 판단 기준에는 정확성, 명확성, 수행량, 메모리 사용량, 최적성 등이 있다.
정확성 : 자료 입력 시 유한한 시간 내에 올바른 결과를 출력
명확성 : 알고리즘의 표현이 이해하기 쉽고 명확하게 작성
수행량 : 일반적인 연산을 제외하고 알고리즘의 특성을 나타내는 중요 연산을 분석
메모리 사용량 : 명령어, 변수, 입출력 자료와 정보를 저장하기 위한 메모리 사용 정도 판단
최적성 : 사용 환경에 따른 수행량과 메모리 사용량 변화에 대한 최적화를 판단이러한 기준을 바탕으로 알고리즘을 분석하는 방법에는 실행에 필요한 공간적 측면에서 분석하는 공간 복잡도, 소요 시간 측면의 시간 복잡도가 있다. 이 포스팅에서는 시간 복잡도를 나타내는 Big-O(빅오) 표기법과 간단한 예제들을 다룬다.
Big-O(빅오) 표기법
시간 복잡도 함수에서 불필요한 정보를 제거하여 알고리즘 분석을 쉽게 할 목적으로 시간 복잡도를 표시하는 방법을 Big-O(빅오) 표기법이라고 한다. Big-O에서는 최악의 상황을 가정하여 연산 횟수를 짐작한다.
1️⃣ O(1) : Constant Time
입력 데이터의 크기에 상관없이 일정한 시간이 걸린다면 O(1)의 시간 복잡도를 가진 알고리즘(Constant Time)이라고 한다. 어떤 배열이 있다고 할 경우, 배열의 길이와 상관없이 해당 index에 접근해 즉시 값을 얻을 수 있다.
// C
int arr[3] = {0,1,2};
void printArr(int arr[]) {
printf("%d\n", arr[0]);
printf("%d\n", arr[1]);
printf("%d\n", arr[2]);
}
int main(void) {
printArr(arr);
}// Javascript
function printArr(arr, index) {
return arr[index]
}
const arr = [0, 1, 2]
console.log(printArr(arr, 0))
console.log(printArr(arr, 1))
console.log(printArr(arr, 2))2️⃣ O(log n) : Logarithmic Time
O(log n)은 로그 복잡도(Logarithmic Time)라고 부르며, Big-O표기법중 O(1) 다음으로 가장 빠르다.
다음 코드는 i = i * 2 에 의해 1, 2, 4, 8, 16 ...인 2의 거듭제곱으로 증가한다. 이는 log2 N번 연산하므로, 시간 복잡도는 O(log n)이다.
// C
void printNum(int n){
int i = 1;
while(i < n){
printf("%d\n", i);
i = i * 2;
}
}
int main(void) {
printNum(20);
}// Javascript
function printNum(n) {
let i = 1
while (i < n) {
console.log(i)
i = i * 2
}
}
printNum(20)이진 탐색(Binary Search)의 경우 또한 O(log n)의 시간 복잡도를 가진다. 찾고자 하는 값을 정렬된 배열의 중간 값과 비교하여 절반을 탐색 대상에서 제외시키기 때문이다.
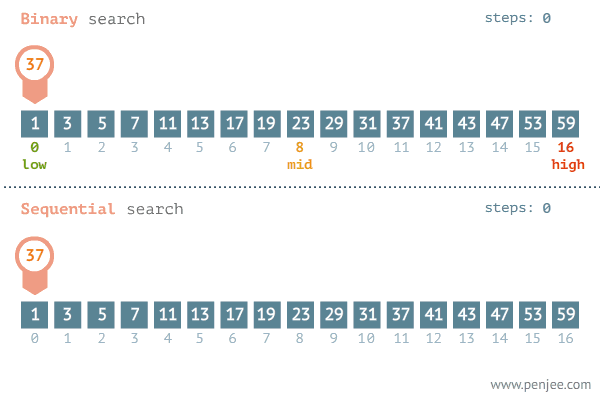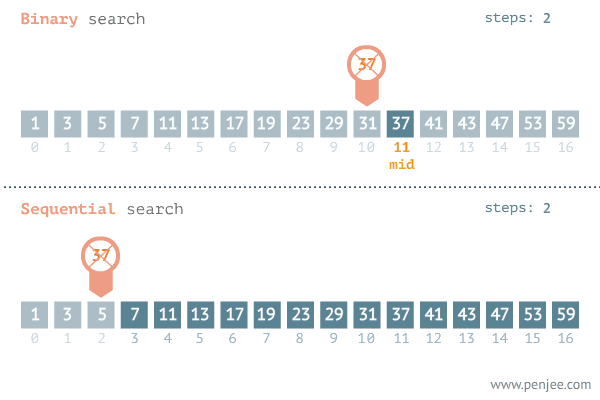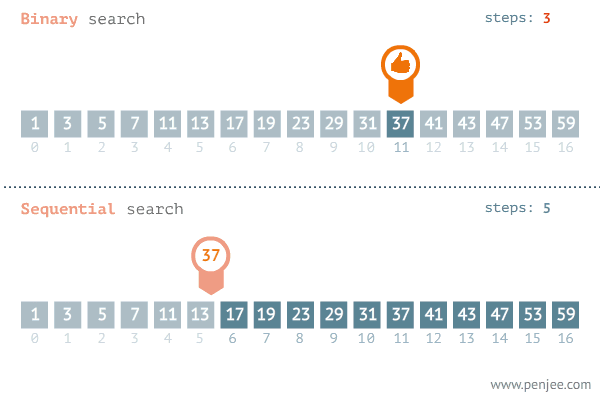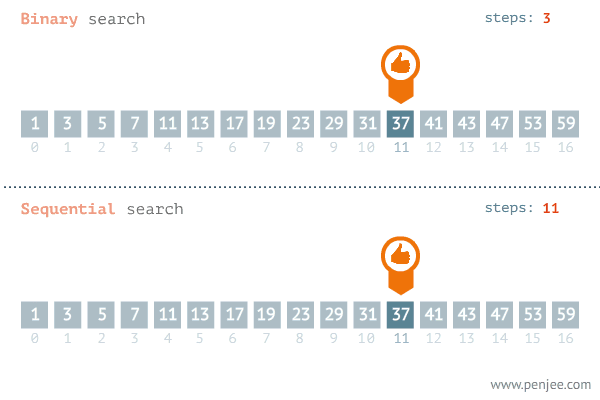
3️⃣ O(n) : Linear Time
입력 데이터의 크기에 비례해서 처리시간이 늘어나는 경우 O(n)이다. 입력된 값이 1일 때의 시간이 1초 걸린다면, 입력된 값이 100일 때 100초일 것이다.
// C
void printNum(int n){
for (int i=0; i < n; i++) {
printf("%d\n", i);
}
}
int main(void) {
printNum(10);
}// Javascript
const arr = ["a", "b", "c", "d"]
function printArr() {
for (let i = 0; i < arr.length; i++) {
console.log(`arr[${i}] = ${arr[i]}`)
}
}
printArr(10)4️⃣ O(n log n) : Linearithmic Time
위에서 다룬 O(log n)의 시간복잡도를 가진 while문에 for문이 중첩된 구조이다. for문의 반복횟수는 n에 비례하는 반면, while문의 반복횟수는 log n에 비례한다.
// C
void printNum(int n){
for(int i=1; i<n; i++){
int j=1;
while(j<n){
printf("%d %d\n",i,j);
j = j * 2;
}
}
}
int main(void) {
printNum(10);
}// Javascript
function printNum(n) {
for (let i = 0; i < n; i++) {
let j = 1
while (j < n) {
console.log(`${i} x ${j} = ${i * j}`)
j = j * 2
}
}
}
printNum(5)5️⃣ O(n^2) : Quadratic Time
이중 for문을 돌면서 수행하는 알고리즘은 O(n^2)의 시간 복잡도를 갖는다. 입력 데이터가 증가함에 따라 시간이 n의 제곱수의 비율로 증가한다. 2 이상의 제곱이 주어져도 영향력이 미비하기 때문에 통상적으로 O(n^2)으로 표시한다.
// C
void printNum(int n){
for(int i=1; i<=n; i++){
for(int j=1; j<=n*2; j++) {
printf("%d %d\n", i, j);
}
}
}
int main(void) {
printNum(3);
}// Javascript
function multiplication(n, m) {
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= m; j++) {
console.log(`${i} x ${j} = ${i * j}`)
}
console.log()
}
}
multiplication(9, 9)6️⃣ O(2n) : Exponential Time
O(2n)은 Big-O(빅오) 표기법 중에서 O(n!)을 제외한다면 가장 느리며, 입력 데이터가 어느 정도 커지면 소요 시간은 무한대에 가까워질 수 있다. 대표적으로 재귀적 수행을 하는 피보나치 수열이 있다.
10870번: 피보나치 수 5 | Baekjoon Online Judge
function fibonacci(input) {
if (input == 0) return 0
else if (input == 1) return 1
else return fibonacci(input - 1) + fibonacci(input - 2)
}
console.log(fibonacci(input))7️⃣ O(n!) : Factorial Time
Big O 최악의 런타임이다. 입력 데이터의 원소들로 만들 수 있는 모든 순열을 생성한다.
다음 코드는 Factorial Time에 대한 정의이다.
void nFacRuntimeFunc(int n) {
for(int i=0; i<n; i++) {
nFacRuntimeFunc(n-1);
}
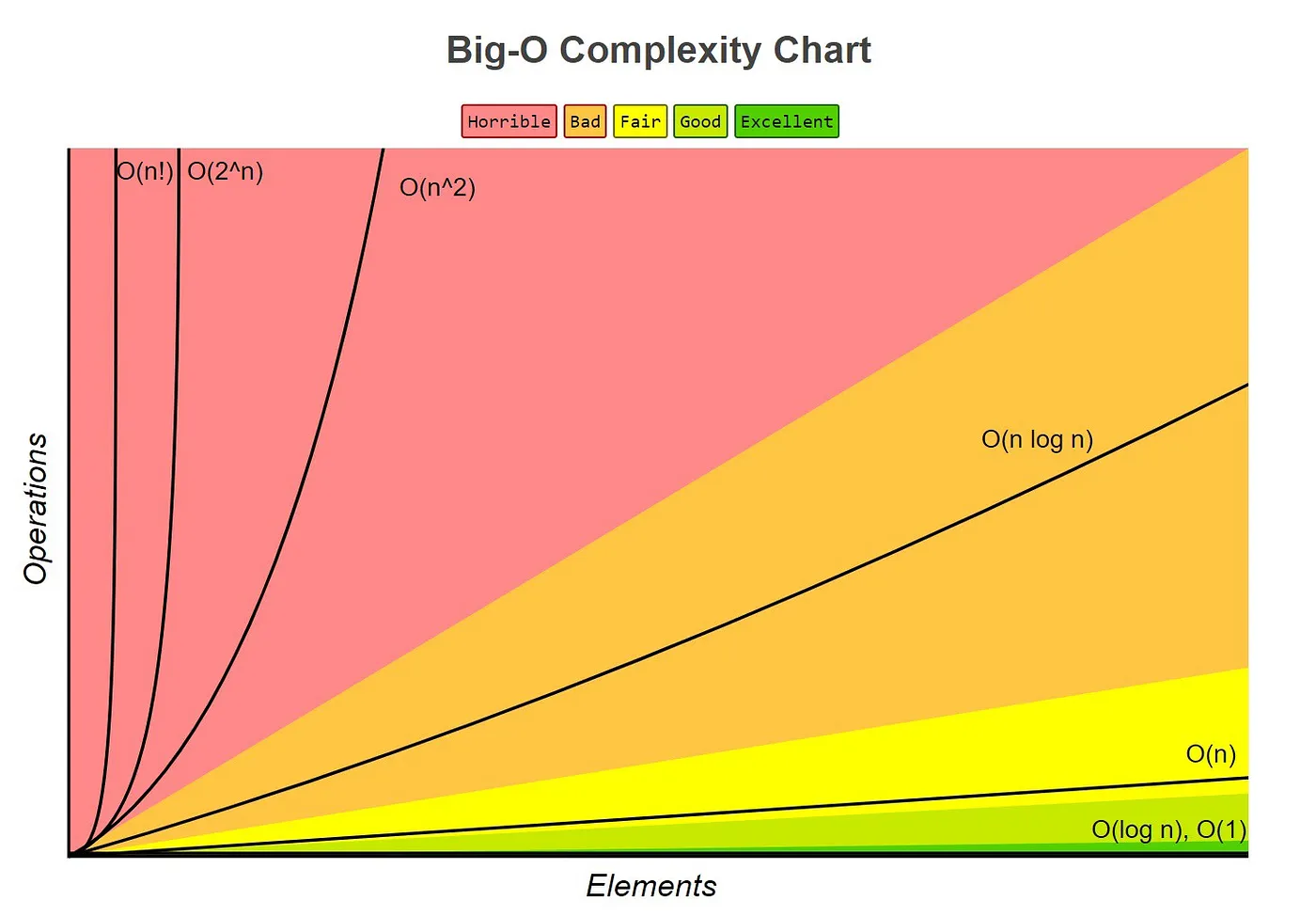
}시간 복잡도 그래프
속도는 O(1) O(log N) O(N) O(N log N) O(N^2) O(2^N) O(N!) 순서대로 빠르다.
Reference
Time Complexity and BigO Notation... | by Sebastian De Lima
Big-O Algorithm Complexity Cheat Sheet (Know Thy Complexities!) @ericdrowell