여행하는 외판원 문제(TSP : Traveling Salesman Problem)는 모든 도시들을 단 한 번만 방문하고 원래 출발한 도시로 돌아오는 최단 경로를 알아내는 문제이다. 이번 포스트는 다음과 유사한 문제를 최근접 이웃 알고리즘(Nearest Neighbor Algorithm)을 통해 구현했던 프로젝트에 대해 다루었다.
여행하는 외판원 문제
어느 외판원이 자신의 사무실에서 출발하여 여러 곳의 방문지를 들려 판매 상담을 진행하려 한다. 모든 업무가 끝나면 사무실로 복귀한다. 일을 빠르게 마치려면 들려야 하는 방문지들을 최대한 효율적으로 빠르게 순회해야 할 것이다. 이것이 바로 외판원 문제(TSP : Traveling Salesman Problem)이다. 이 문제는 최단 경로를 구해야 하는 경우 NP-난해에 속하며, 흔히 계산 복잡도 이론에서 해를 구하기 어려운 문제의 대표적인 예로 많이 다룬다.
최근접 이웃 알고리즘
외판원 순회의 경우 문제들 중에서도 어려운 편으로, 일반적인 외판원 문제에 대한 다항 시간 근사 알고리즘은 P=NP가 아닌 한 존재하지 않는다는 것이 밝혀져 있다. 표본의 수가 증가함에 따라 경우의 수가 기하급수적으로 늘어나 다항식 시간 내에 풀 수 있는 알고리즘이 없으므로 근사 해를 구하는 것이 일반적이다. 최적에 가까운 해를 구하는 데 사용할 방법 중 하나로 근사 알고리즘을 사용하는 것이 있다. 이러한 알고리즘은 최적에 가깝지만 반드시 최적은 아닌 솔루션을 제공한다. 잘 알려진 근사 알고리즘 중 하나는 최근접 이웃 알고리즘(Nearest Neighbor Algorithm)이다.
이 방법은 탐욕 알고리즘(Greedy algorithm)에 기초한다. 최적해를 구하는 데 사용하는 근사적인 방법으로, 경우의 수를 결정하는 순간마다 최적의 방법을 선택해 나가며 크기가 큰 문제에서 작은 문제로 줄여나가는 하향식 방법으로 진행한다.
관광 경로 만들기
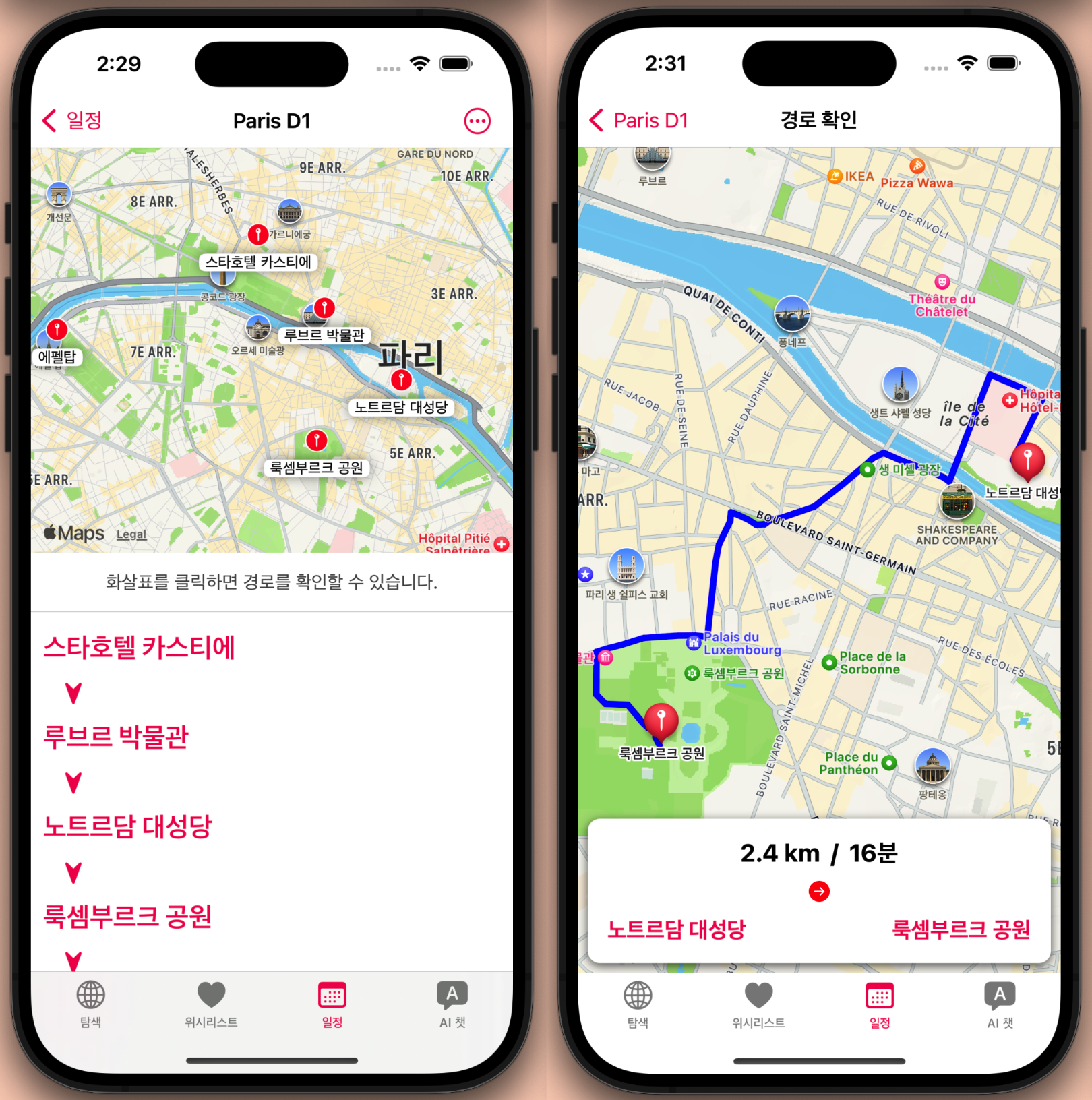
최근접 이웃 알고리즘을 적용해 볼 문제는 다음과 같다. 출발지와 도착지가 되어질 '숙소'가 주어지고, 방문하려 하는 여러 개의 '관광지'가 주어진다. 이를 여행할 최적의 경로로 만들면 된다.
// dict 배열 예시
const dict = [
{
id: 1, // 숙소
lat: 48.86836127133744,
lon: 2.3268056623807514,
},
{
id: 2, // 관광지 1
lat: 48.85836985229897,
lon: 2.2944622771397345,
},
{
id: 3, // 관광지 2
lat: 48.860632246610514,
lon: 2.3374079634624687,
},
...
];const startPoint = dict[0]
const remainingPoints = dict.slice(1)
nearestNeighbor(startPoint, remainingPoints)
function nearestNeighbor(start, points) {
// 결과 배열 초기화 및 남은 지점 배열 생성
const result = [start]
const remainingPoints = [...points]
while (remainingPoints.length > 0) {
let nearestIndex = 0
let nearestDistance = haversineDistance(
start.lat,
start.lon,
remainingPoints[0].lat,
remainingPoints[0].lon
)
// 최근접 지점 찾기
for (let i = 1; i < remainingPoints.length; i++) {
const distance = haversineDistance(
start.lat,
start.lon,
remainingPoints[i].lat,
remainingPoints[i].lon
)
if (distance < nearestDistance) {
nearestIndex = i
nearestDistance = distance
}
}
// 최근접 이웃을 다음 출발점으로 설정하고 결과에 추가
start = remainingPoints[nearestIndex]
result.push(start)
remainingPoints.splice(nearestIndex, 1)
}
return result
}
// 모든 지점 설정 완료까지 반복start, points 파라미터는 숙소, 관광지의 id 값과 위도, 경도 값을 받는다. startPoint로 배열의 첫 번째 요소를 지정, remainingPoints에 거리를 비교할 나머지 요소들을 지정하고, 최근접 지점을 찾아내는 nearestNeighbor 함수가 startPoint에서 갈 곳을 선택한다. 이를 반복해 나가며 경로를 구성하는 원리이다.
Haversine Formula
// Haversine Formula : 경도와 위도가 주어진 두 지점 사이의 대원 거리를 계산
function haversineDistance(lat1, lon1, lat2, lon2) {
// 지구 반경 상수 (단위: km)
const earthRadius = 6371
// 각도를 라디안으로 변환
const dLat = toRadians(lat2 - lat1)
const dLon = toRadians(lon2 - lon1)
// Haversine 공식 계산
const a =
Math.sin(dLat / 2) * Math.sin(dLat / 2) +
Math.cos(toRadians(lat1)) *
Math.cos(toRadians(lat2)) *
Math.sin(dLon / 2) *
Math.sin(dLon / 2)
const c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a))
// 대원 거리 계산 및 소수점 둘째 자리까지 반환
const distance = (earthRadius * c).toFixed(2)
return distance
}
// 각도를 라디안으로 변환하는 함수
function toRadians(degrees) {
return (degrees * Math.PI) / 180
}하버사인 공식(Haversine Formula)은 두 지점 사이의 구면적 거리(원형 지구 상에서의 거리)를 구하는 데 사용되는 공식이며 지구의 구면성을 고려하여 위도와 경도를 기준으로 두 지점 사이의 최단 거리를 구할 때 주로 사용된다. 이를 통해 두 지점 간의 거리를 계산하여 최근접 지점을 비교하는 데 사용하였다.
이 공식은 일반적인 사용에서는 큰 무리는 없을 정도이지만, 실제 지구는 적도 쪽이 좀 더 길쭉한 타원형이기 때문에 완벽히 정확한 값이라고 할 수는 없다. 또한 이러한 방법은 두 좌표의 직선 거리를 구하게 되기 때문에 실제 도로 주행을 했을 때의 길이와 차이가 발생한다. 가급적이면 주행할 거리 간의 비교를 통한 최근접 이웃 연산이 더욱 정확할 것이다. 납득할 수 있는 효율적인 경로를 만들어 볼 수는 있었지만, 보다 더 최적에 가까운 값을 찾기 위해서는 다른 방법을 찾아봐야 할 것이다.
Reference
Traveling Salesman Problem: Nearest Neighbor Algorithm Solution