알고리즘 문제의 복잡성에 대해 이야기할 때, P-NP, NP-완전, NP-난해와 같은 용어들이 등장하게 된다. 외판원 순회, 부분집합의 합과 같은 문제들에 대해 찾아볼 때 각 정보글마다 NP-완전이니, NP-난해니 말이 달라서 혼란이 있었다. 이에 대해 좀 더 조사해 보니, 그렇게 헷갈리게 된 원인이 파악되었다. 이 포스트에서는 P-NP의 개념과 함께 NP-난해 (NP-hard)와 NP-완전 (NP-complete)의 차이를 명확히 하고, 추가적으로 외판원 순회 문제의 두 가지 종류에 대한 내용도 다루었다.
P와 NP
먼저 이 개념은 결정론적, 비결정론적 튜링 머신과 관련되어 있다. 튜링 머신 (Turing machine)은 수학자 앨런 튜링(Alan Turing)이 1936년에 제시한 개념으로, 계산하는 기계의 일반적인 개념을 설명하기 위한 가상의 기계다. 튜링은 이 개념을 Automatic에서 따온 A-Machine이라고 불렀는데 튜링 사후에 창시자의 이름을 따 튜링 머신이라고 부르게 되었다.
따라서 튜링 머신은 실존하는 기계가 아니라 수학적 상상이다.
- 결정론적 튜링 머신: 매 순간 다음 상태를 하나만 가질 수 있다.
- 비결정론적 튜링 머신: 매 순간 여러 개의 다음 상태를 가질 수 있다.
P (Polynomial Time)는 결정론적 튜링 머신이 다항 시간 내에 풀 수 있는 문제들의 집합이다. 다항식(Polynomial) 시간 이내에 그 문제의 답을 계산해낼 수 있는 알고리즘이 존재한다면, 그 문제는 P 문제에 해당된다. 결론적으로 네, 아니오로 명확히 대답할 수 있고, 답을 찾는 것에 그리 오랜 시간이 걸리지 않는다.
NP (Non-Deterministic Polynomial Time)는 비결정론적 튜링 머신이 다항 시간 내에 풀 수 있는 문제들이다. 문제를 푸는 각 단계에서 여러 가지의 가능성을 동시에 고려할 수 있는 비결정적 알고리즘(Non-Deterministic Algorithm)으로, 이는 '알맞은 힌트'를 주면 다항 시간 내에 검증할 수 있는 문제로 생각할 수도 있다. 따라서 NP는 풀이가 힘들 수 있지만, 답이 맞는지는 확인할 수 있는 문제다.
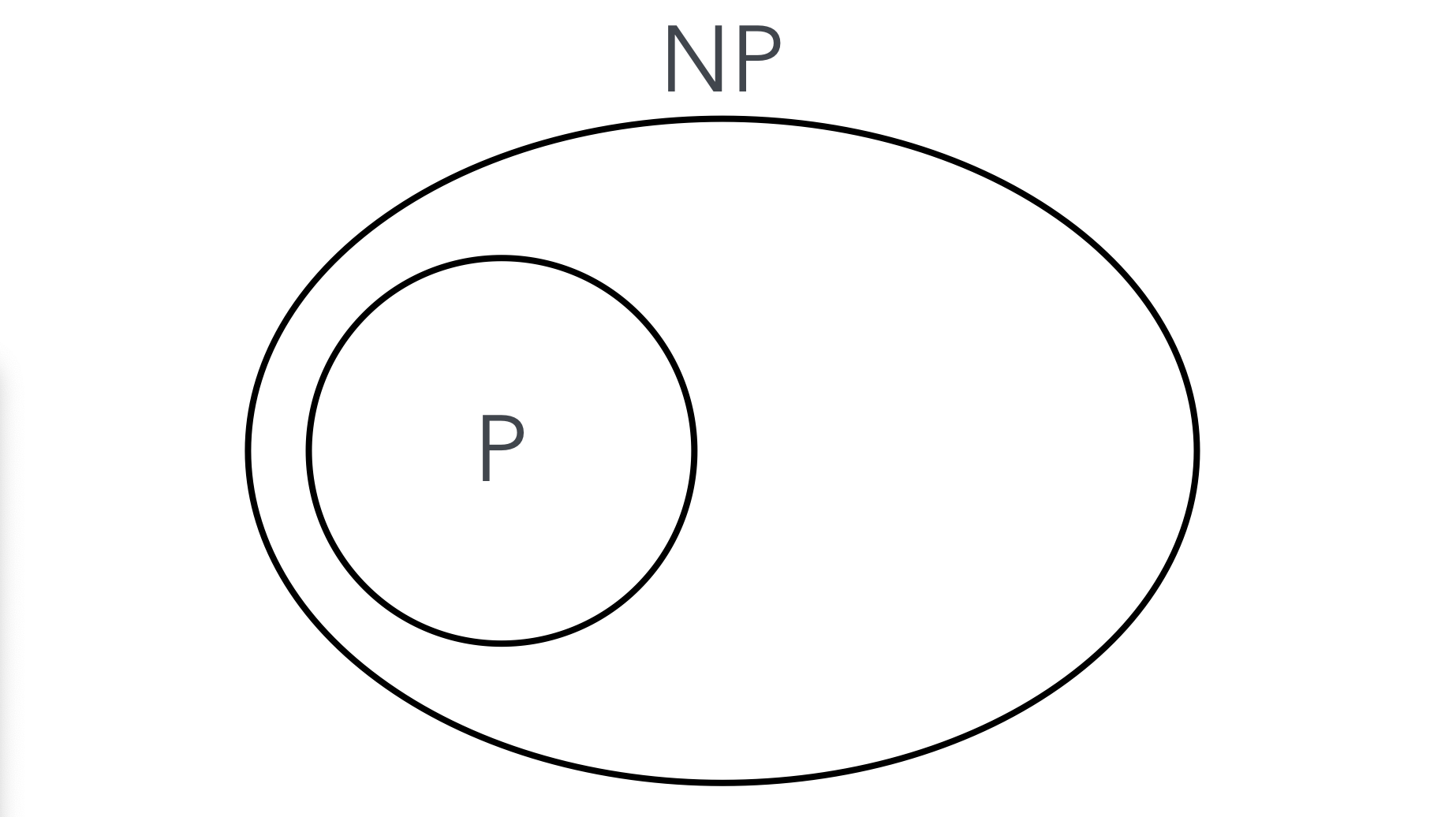
P는 NP에 포함되며, 모든 P 문제는 NP 문제다. NP 문제 중 일부는 아직 결정론적 튜링 머신으로 다항 시간 내에 풀 수 있는지(즉, P에 속하는지) 불확실하다.
NP-난해 (NP-Hard)
다음은 NP 문제에 대한 문제 포함 관계 그림이다. 아직 완전히 증명되지는 못했으나, 대부분의 전문가들에 의해 이 형태가 맞을 것으로 추정하고 있다고 한다.
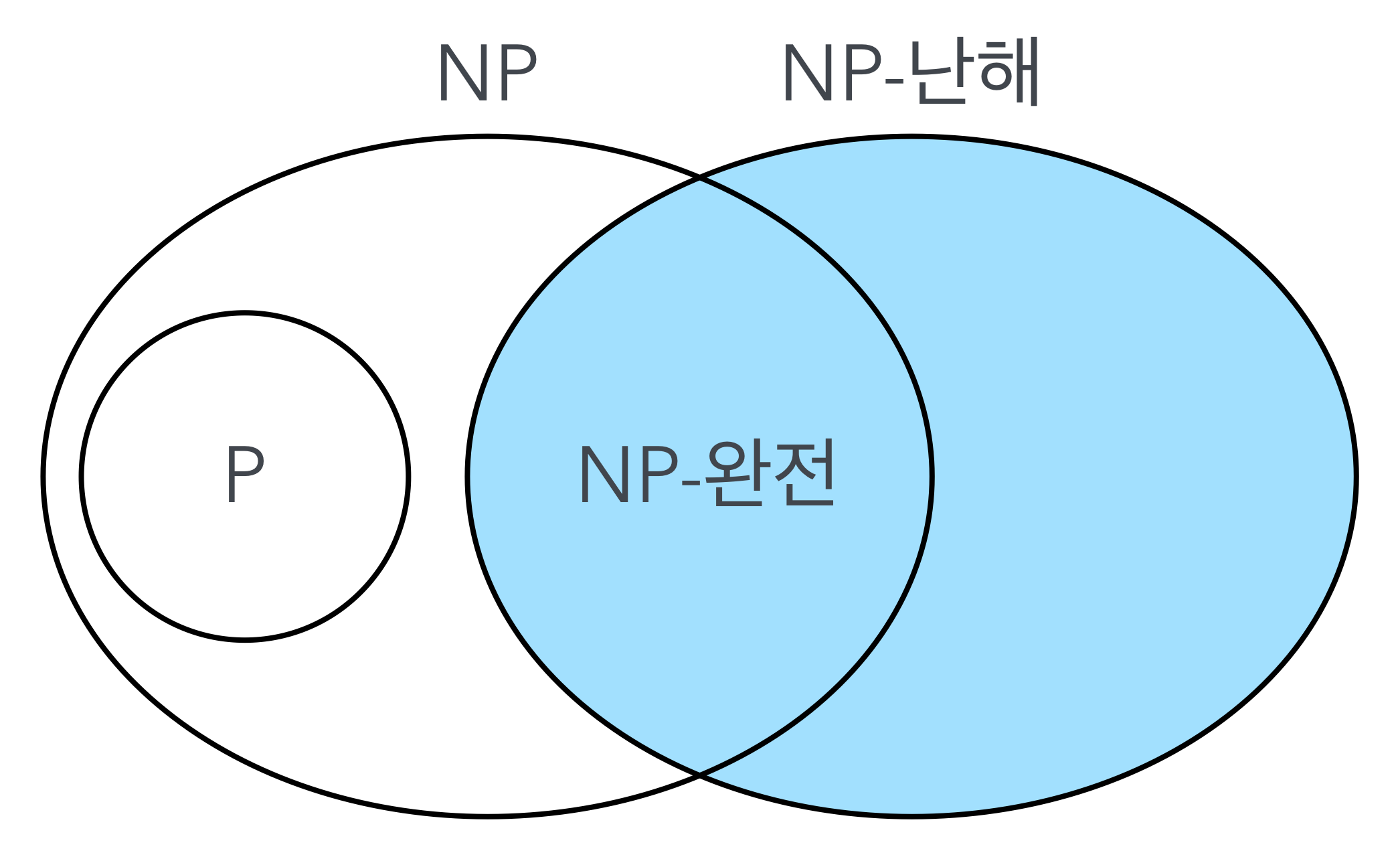
NP-난해 (NP-Hard)는 NP 문제를 포함한 더 어려운 문제까지 포괄하는 개념으로, 주어진 답을 빠르게 검증할 수 있는지 여부와 관계없이 모든 NP 문제를 이 문제로 변환할 수 있는 문제이다. 적어도 모든 NP 문제만큼은 어려운 문제들의 집합이다.
즉, 어떤 NP-난해 문제를 풀 수 있다면, 모든 NP 문제도 다항 시간 내에 풀 수 있다는 의미다. 하지만 NP-난해 문제는 NP에 속하지 않을 수도 있어, 검증조차 다항 시간 내에 불가능할 수 있다. NP-난해 문제들은 보통 근사나 휴리스틱한 방법 등 간접적으로 해결된다.
주요 NP-난해 문제
외판원 순회(Traveling Salesman Problem) (최적화 버전)
정지 문제(Halting Problem)
부분 집합의 합(Subset Sum) (NP-완전에도 속함)NP-완전 (NP-Complete)
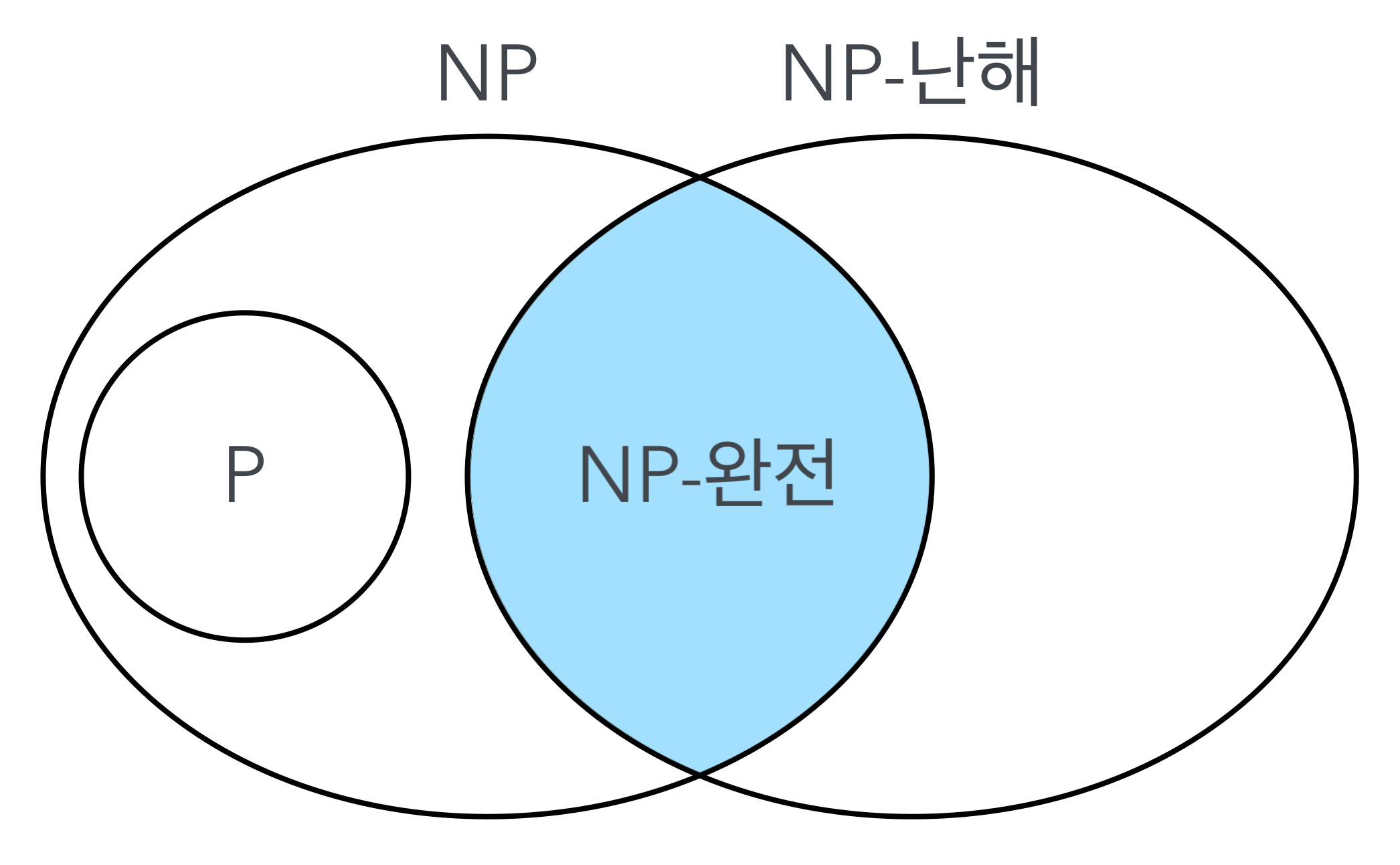
NP-완전 (NP-Complete)는 NP-난해 문제의 하위 집합으로, NP에 속하면서 NP 난해인 문제이다. 해결 방법이 주어졌을 때 빠르게(다항 시간 내에) 검증할 수 있으며, 다른 모든 NP 문제를 다항 시간 내에 변환할 수 있는 문제를 뜻한다.
NP-완전 문제를 풀 수 있는 알고리즘이 존재한다면, 모든 NP 문제를 풀 수 있는 알고리즘도 존재한다는 뜻이다. 따라서 NP-완전 문제는 NP와 P의 관계를 이해하는 데 매우 중요하다.
주요 NP-완전 문제
외판원 순회(Traveling Salesman Problem) (결정형 버전)
해밀턴 경로(Hamiltonian Path)
충족 가능성 문제(Satisfiability Problem)난해와 완전이 혼용되어 사용된 이유
어떠한 알고리즘 문제에 대해 A 글에서는 NP-완전 문제이다... B 글에서는 NP-난해 문제이다... 표현이 다르면 이 개념에 대해 처음 배우게 될 때 굉장한 혼란이 될 수 있다.
부분집합의 합 문제
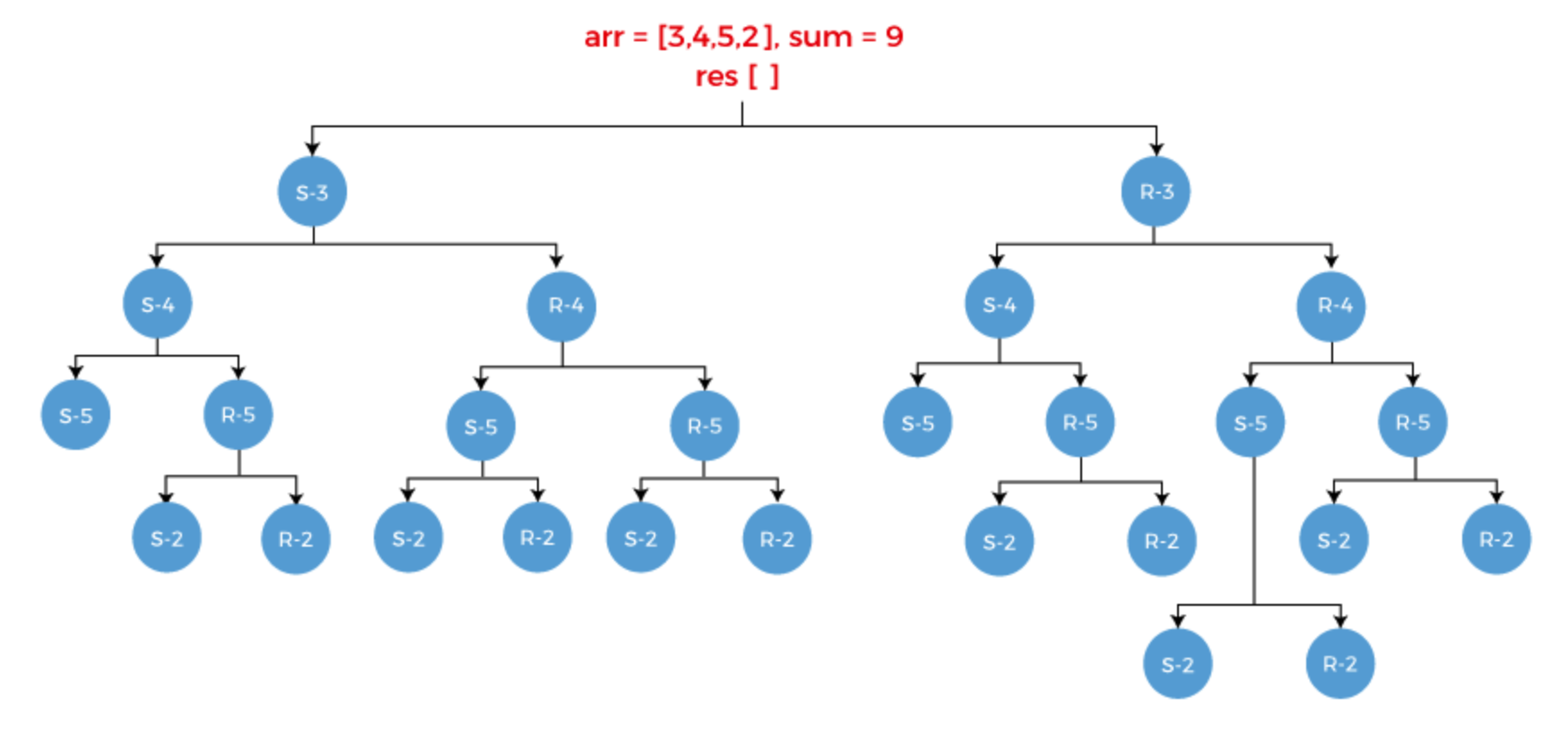
NP-난해에 해당하는 문제 중 부분집합의 합 문제(Subset Sum)가 있다. 이 문제는 계산 복잡도 이론과 암호학에 관련된 문제로, n개의 원소를 가진 정수의 집합 S가 주어지고, 임의의 정수 K가 주어졌을 때, 합이 K가 되는 부분집합이 있는지를 묻는 문제이다. 기본적으로 NP-완전 문제라 볼 수 있지만, 부분집합의 합 문제를 다룬 여러 정보글에서 NP-난해, NP-완전을 혼용하여 사용한 것이 확인되었다.
앞서 다룬 개념대로 보자면 1차적으로 NP-완전 문제는 NP-난해 문제의 하위 집합이다. 문제를 다루기에 앞서 NP-난해와 NP-완전의 문제 포함 관계에 대해 정의하고 들어가거나, Subset Sum 문제는 NP-난해이면서 NP-완전 문제이다. 라고 명시하는 것이 옳게 된 표현이다.
최적화, 결정형 외판원 순회 문제
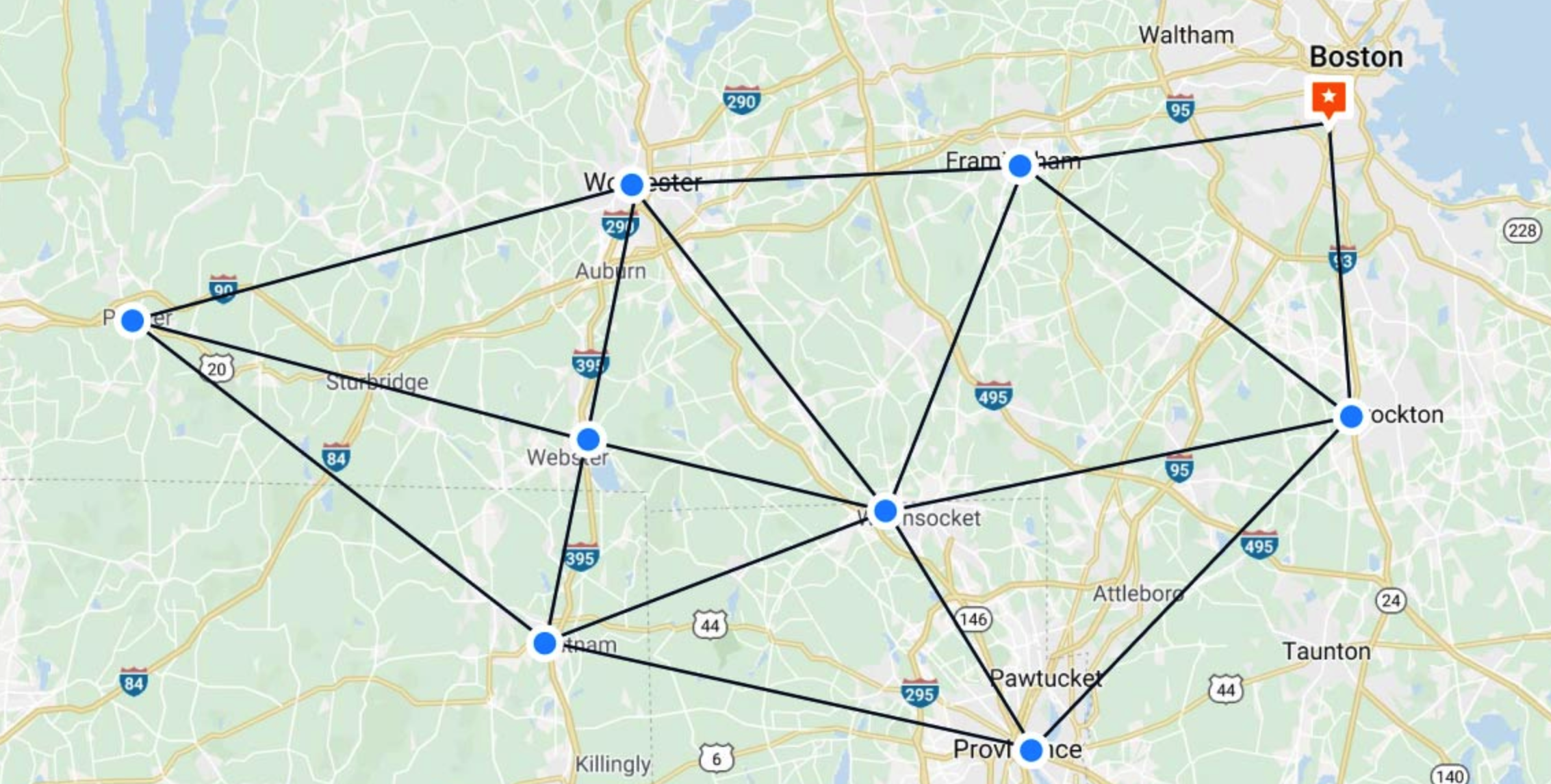
외판원 순회 문제(Traveling Salesman Problem)는 주어진 모든 도시를 한 번씩 방문하고 다시 시작 도시로 돌아오는 경로에 대한 문제이다.
보통의 외판원 순회 문제는 각 도시의 최소 여행 경로를 찾는 것을 원하므로, 이 경우는 NP-난해에 해당한다. 최적해를 찾는 경우(최적화 버전, Optimization Version)인 것이다.
최단 경로가 아닌 특정한 조건을 원하는 경우의 형태도 있다. 가중치의 합이 어떤 값 이하인 것이라던가. 이러면 결정형 버전(Decision Version)이 된다. 이는 최적화 문제로서의 외판원 순회 문제와 달리, 경로의 길이가 특정 임계값 이하인지를 확인하는 형태로 바뀌었기 때문에 NP-완전의 조건을 만족한다.
두 가지 버전을 예시와 함께 정리해 보면 다음과 같다.
- 외판원 순회 문제(최적화 버전) : 한 도시에서 출발하여 모든 도시를 한 번씩 방문하고 다시 출발지로 돌아오는 최소 비용의 경로를 찾는 문제이다.
- 외판원 순회 문제(결정형 버전) : 주어진 비용 C 이하로 모든 도시를 한 번씩 방문하고 다시 출발지로 돌아오는 경로가 존재하는지를 묻는 문제로, "모든 도시를 한 번씩 방문하고 다시 출발지로 돌아오는 경로의 총 비용이 C 이하인 경로가 존재하는가?"라는 질문을 하는 것이다.
따라서 통상적인 외판원 순회에서 변형된 버전은 NP-완전이 될 수 있다. 외판원 순회는 문제들 중에서도 어려운 편으로, 일반적인 외판원 순회 문제에 대한 다항 시간 근사 알고리즘은 P = NP가 아닌 한 존재하지 않는다는 것이 밝혀져 있다.