백트래킹(Backtracking)은 해결할 문제에 대한 해답 후보를 체계적으로 탐색하는 알고리즘적 기법이다. 가지치기(Pruning)를 통해 불필요한 연산을 줄여가며 점진적으로 해를 찾아가는 방식으로, 특히 조합 탐색(Combination Search)과 같이 탐색 범위가 넓은 문제에서 큰 효과를 발휘한다.
백트래킹(Backtracking)
백트래킹은 모든 가능한 해답 후보를 탐색하되, 가능한 가지를 모두 뻗어 나가면서도 ‘이 경로는 답이 되기 어렵다’고 판단되는 순간 탐색을 중단(Pruning)하는 방식을 사용한다. 즉, 완전 탐색(Brute Force)의 변형으로, 조건을 만족하지 않는 경로는 더 이상 진행하지 않는 “가지치기” 방법을 통해 불필요한 시도를 줄이는 것이다. 완전 탐색보다 훨씬 효율적인 경우가 많지만, 여전히 최악의 경우 시간 복잡도가 매우 커질 수 있다는 점을 유의해야 한다.
백트래킹은 재귀(Recursion) 기반으로 동작하는 경우가 많다. 단계별로 해답 후보를 하나씩 결정하면서 조건에 어긋나면 되돌아가는(Backtrack) 과정을 반복한다. 흔히 해결 대상이 되는 문제는 다음과 같다.
- 모든 도시를 방문하는 경로를 찾아야 하는 여행하는 외판원 문제(TSP)
- 모든 빈 칸에 숫자를 채워야 하는 스도쿠(Sudoku)
- 특정 조건을 만족해야 하는 N-Queen 문제 등
이 때, 백트래킹은 다음과 같은 절차로 진행된다.
- 해답 후보를 하나 선택한다.
- 현재 후보가 문제의 조건을 만족하지 않으면(가지치기) 뒤로 돌아간다.
- 만족한다면 다음 단계로 넘어가 새로운 해답 후보를 선택한다.
- 모든 단계를 처리하고 마지막까지 조건을 만족하면 전체 해가 된다.
여행 경로 찾기에 백트래킹 적용하기
이번 예시에서 적용할 백트래킹 방식은 이전에 다루었던 문제를 변형해 본 것으로, 일반적으로 소개되는 백트래킹을 통한 TSP 문제 유형과는 다소 다를 수 있다.
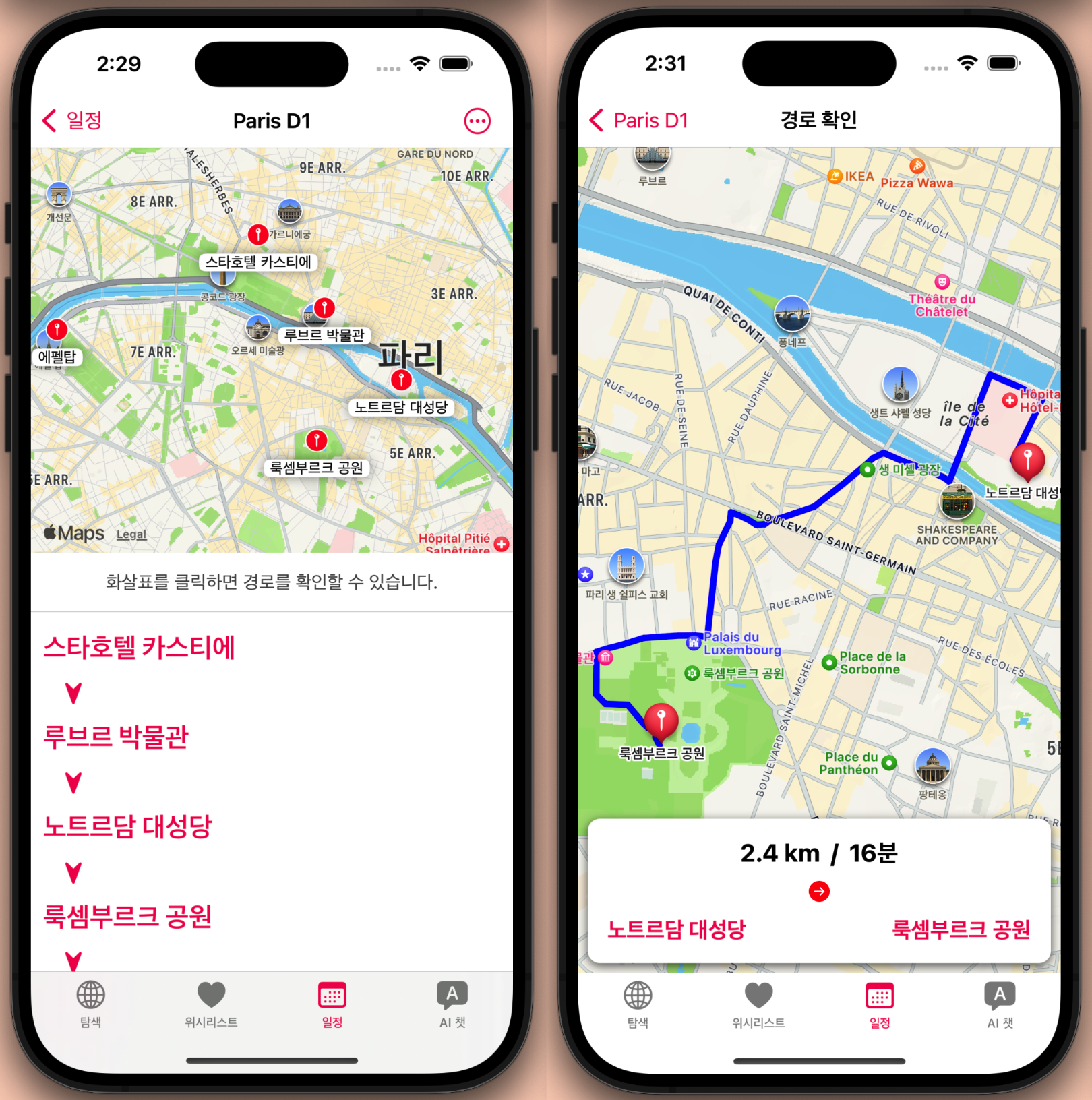
최적의 여행 경로를 찾기 위한 최근접 이웃 알고리즘 솔루션
최근접 이웃 알고리즘(Nearest Neighbor Algorithm)은 탐욕적인 방식으로 ‘가장 가까운 장소부터 찾아가는’ 전략을 택해 빠르게 경로를 구성했었다. 이 방식은 매우 심플하지만, 항상 전역적으로 최적인 해답을 보장하지는 않는다.
백트래킹을 적용하면, 모든 경로를 탐색하면서 “더 이상 최적일 수 없는 지점”에서는 해당 분기를 중단하고 이전 단계로 돌아간다. 단순한 형태의 외판원 문제(TSP) 예시 코드를 살펴보면 다음과 같이 구성할 수 있다.
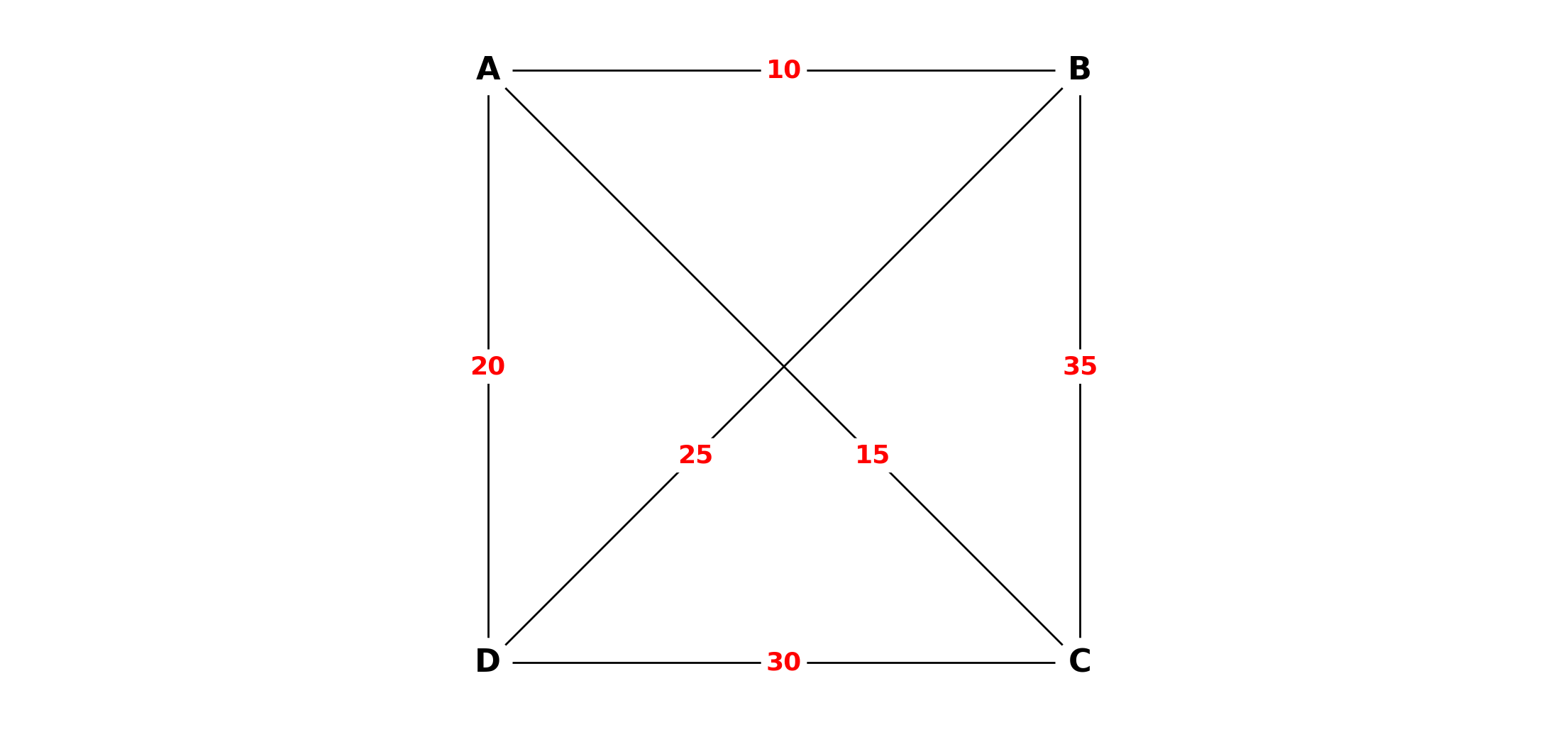
// 예시 데이터 (여기서는 위도/경도 대신 단순 거리로 가정)
const distanceMatrix = [
// A B C D
[0, 10, 15, 20], // A
[10, 0, 35, 25], // B
[15, 35, 0, 30], // C
[20, 25, 30, 0], // D
]
const visited = new Array(distanceMatrix.length).fill(false)
let bestPath = [] // 최적 경로
let minDistance = Infinity // 최단 거리, 가지치기를 위해 초기값은 일단 Infinity로 설정
function backtrack(currentNode, depth, path, currentDistance) {
// 모든 노드를 방문한 경우, 시작점으로 돌아온 거리까지 포함해 경로 갱신 여부 확인
// 현재 도시(currentNode), 현재까지 방문한 도시 수(depth), 경로(path), 현재까지의 총 거리(currentDistance)
if (depth === distanceMatrix.length) {
const totalDistance = currentDistance + distanceMatrix[currentNode][0]
if (totalDistance < minDistance) {
minDistance = totalDistance
bestPath = [...path, 0] // 순회를 마치고 시작점(0)으로 돌아옴
}
return
}
for (let nextNode = 0; nextNode < distanceMatrix.length; nextNode++) {
// 이미 방문한 노드는 생략
if (visited[nextNode]) continue
// 이동 거리 계산
const nextDistance = currentDistance + distanceMatrix[currentNode][nextNode]
// 현재까지의 거리가 이미 기존 최소 거리보다 큰 경우, 더 갈 필요가 없으므로 가지치기
if (nextDistance >= minDistance) continue
// 아직 최적 경로가 될 가능성이 남아 있다면, nextNode 방문 처리 후 재귀 호출
visited[nextNode] = true
backtrack(nextNode, depth + 1, [...path, nextNode], nextDistance)
visited[nextNode] = false
}
}
// 시작점을 0(도시 A)이라고 가정하고, 방문 표시(visited[0] = true)를 해둔 뒤 시작
visited[0] = true
backtrack(0, 1, [0], 0)
console.log("최적 경로:", bestPath)
console.log("최소 거리:", minDistance)위 예시는 하나의 단순화된 스니펫으로, 실제로는 A, B, C, D 각 노드(도시)를 모두 방문한 뒤 다시 A로 돌아오는 최소 거리를 찾는 방식이다. 기본 아이디어는 다음과 같다.
- 시작점(0번 노드)에서 출발한다.
- 다음에 방문할 노드를 정하기 위해 모든 노드를 시도한다.
- 이미 방문한 노드는 건너뛰며, 현재 누적 거리 + 이동 예정 거리가 기존에 찾은 최소 거리(minDistance)보다 커지면 가지치기(pruning)한다.
- 모든 노드를 방문한 뒤, 다시 시작점으로 돌아오는 경로 거리를 확인하고, 더 작다면 최소 거리를 갱신한다.

A(0) → B(1) → D(3) → C(2) → A(0) 순으로 방문할 때 총 이동 거리가 80이 되며, 이것이 최단 경로로 확인된다.
이처럼 백트래킹은 모든 가능한 경로를 시도하면서도, 불필요하게 긴 경로는 애초에 더 이상 진행하지 않는다. 최근접 이웃 알고리즘처럼 빠른 결정을 통해 빠르게 경로를 찾아내지는 못하지만, 전 탐색을 기반으로 더 정확한(최적에 가까운) 답을 찾을 수 있다는 장점이 있다.
백트래킹은 문제의 모든 해답 후보를 탐색하면서도, 해당 경로가 최적 해가 될 수 없다고 판단되면(또는 문제 조건을 만족할 수 없다고 판단되면) 즉시 탐색을 중단하기 때문에, 완전 탐색보다는 훨씬 효율적이다. 그러나 문제의 크기가 커지면 탐색 공간이 매우 급격하게 늘어날 수 있으므로, 적절한 가지치기 기법을 추가로 적용하거나 다른 근사 알고리즘과 혼용해 사용하는 등의 전략이 필요할 것으로 보인다.